
The bisection method is a popular algorithm for finding a root of.I need an algorithm to perform a 2D bisection method for solving a 2x2 non-linear problem. Finding roots of functions is the heart of algorithms for solving many mathematical problems. The Algorithm The bisection method needs two things to find a root: a continuous function an interval bracketing the desired. Like all numerical root finding algorithms, the method starts with an initial guess and refines it until the root is located within a certain tolerance. The bisection method is a simple and robust root finding algorithm.
The bisection algorithm is a simple method for finding the roots of one-dimensional functions. Assume I already know the solution lies between the bounds x1 Bisection Algorithm. I am very familiar with the 1D bisection ( as well as other numerical methods ).
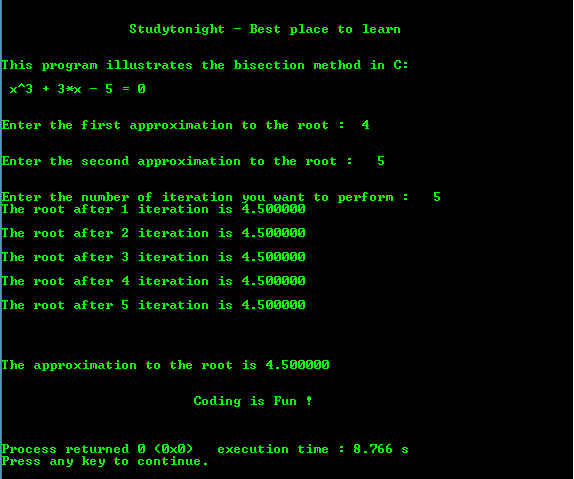
The solution of the problem is only finding the real roots of the equation. The use of this method is implemented on a electrical circuit element. The algorithm starts with a large interval, known to contain x0 x 0, and then successively reduces the size of the interval until it brackets the root.This method is called bisection.
Maybe I am making this a little too complicated, but I think there should be a multidimensional version of the Bisection, just as Newton-Raphson can be easily be multidimed using gradient operators.Any clues, comments, or links are welcomed.I'm not much experient on optimization, but I built a solution to this problem with a bisection algorithm like the question describes. ^Now considering the possibilities of combinations such as checking if f(G)*f(M)<0 AND g(G)*g(M)<0 seems overwhelming. To start the bisection I guess we need to divide the points out along the edges as well as the middle.
Alternativaly you can try other configuration like use the points (E, F, G and H show in the question), but I think make sense to use the corner points because it consider better the whole area of the rectangle, but it is only a impression. It's a bit of redundance but work's well. Compute the minimum product for each one for each direction of variation (axis, x and y).It looks to the product through tow oposite sides of the rectangle and computes the minimum of them, whats represents the existence of a changing of signal if its negative. Calculate the product each scalar function (f and g) by them self at adjacent points. In truth it's generaly a function (x,y) -> (f(x,y), g(x,y)).The steps are the following, and there is a resume (with a Python code) at the end.
But it was more like a guess, I don't now if is the better. I chose eps=2e-32, because 32 bits is a half of the precision (on 64 bits archtecture), then is problable that the function don't gives a zero. In this case the remedy is to incrise eps (increase the rectangles). I the case the functions gives exatly zero at neighbour rectangles (because of an numerical truncation). I thinh it can have tow reasons:

Instead you could divide your quadrilateral recursively, however as it was already pointed out by jpalecek ( 2nd post), you would need a way to stop your divisions by figuring out a test that would assure you would have no zeros inside a quadrilateral. For the 2D case the analytical solution will be a quadratic equation which, according to the solution (1 root, 2 real roots, 2 imaginary roots) you may have 1 solution, 2 solutions, no solutions, solutions inside or outside your quadrilateral.If instead you have analytic functions of f(x,y) and g(x,y) and want to use them, this is not useful.


 0 kommentar(er)
0 kommentar(er)
